Unit 2: Forces, Moments and Static Equilibrium (10hours)
2.1 Types of Forces: External, Internal and Reaction Forces,Point Force, Translational and Rotational Force- Relevant Examples
1. External forces: These are forces acting on an object from its surroundings. Examples include:
- Gravity pulling an apple downward.
- Wind pushing a kite.
- A person pushing a cart.
2. Internal forces: These forces occur within an object and act on its different parts. Examples include:
- Tension in a stretched rope.
- Compression in a compressed spring.
- Shearing forces within a solid material.
3. Reaction forces: These forces occur in response to an external force applied to an object. Examples include:
- The ground pushing back on a person's feet when they jump.
- The recoil force of a gun when a bullet is fired.
- The resistance force of water when swimming.
4. Point force: A force applied at a specific point on an object. Examples include:
- Pushing a door at its handle.
- Poking a balloon with a needle.
- Pressing a button on a keyboard.
5. Translational force: This force causes an object to move in a straight line. Examples include:
- Pushing a car to make it accelerate.
- Kicking a soccer ball to send it rolling.
- Pulling a sled across the snow.
6. Rotational force: Also known as torque, this force causes an object to rotate around an axis. Examples include:
- Twisting a doorknob to open a door.
- Applying force to a wrench to loosen a bolt.
- Spinning a merry-go-round by pushing its rim.
These examples illustrate the different types of forces and their effects on objects in various contexts.
2.2 Resolution and Composition of Forces- Relevant Examples
Resolution and composition of forces refer to the process of breaking down a force into its components or combining multiple forces into a resultant force. Here are some relevant examples:
1. Resolution of forces:
- A force acting at an angle on an object can be resolved into its vertical and horizontal components. For example, if a person pushes a crate diagonally across the floor, the force can be resolved into a vertical force (supporting the weight of the crate) and a horizontal force (causing the crate to move).
- When a force is applied to an inclined plane, it can be resolved into two components: one perpendicular to the plane (normal force) and one parallel to the plane (causing motion along the plane).
2. Composition of forces:
- When two forces act on an object in the same direction, they can be combined by adding their magnitudes. For example, if two people push a car in the same direction with forces of 100 N and 150 N, the resultant force is the sum of the two forces, which is 250 N.
- When two forces act on an object in opposite directions, they can be combined by subtracting their magnitudes. For instance, if a person pulls a suitcase with a force of 50 N and another person pulls it in the opposite direction with a force of 30 N, the resultant force is the difference between the two forces, which is 20 N in the direction of the greater force.
These examples demonstrate how the resolution and composition of forces help analyze and understand the net effect of multiple forces acting on an object.
2.3 Basic Concept of Static Equilibriumand its essence in structuralapplication in civil engineering-Relevant Examples
The basic concept of static equilibrium is crucial in structural applications in civil engineering. It refers to a state where an object or a structure is at rest and all the forces and torques acting on it are balanced, resulting in no net acceleration or rotation. Here are some relevant examples of static equilibrium in civil engineering:
1. Bridges: A bridge is designed to achieve static equilibrium by balancing the forces acting on it. The vertical forces, such as the weight of the bridge and the loads it carries, are countered by the upward reaction forces from the supports or piers. The horizontal forces, such as wind or water currents, are countered by lateral bracing and anchoring systems. By ensuring static equilibrium, the bridge remains stable and can safely support the loads.
2. Buildings: In the design and construction of buildings, static equilibrium is essential to ensure structural stability. The vertical forces, such as the weight of the building and the loads from occupants and contents, are counteracted by the upward reaction forces from the foundation and structural supports. The lateral forces, such as wind or seismic loads, are balanced through the use of structural elements like shear walls, bracing systems, and moment-resisting frames.
3. Retaining walls: Retaining walls are structures used to retain soil or other materials. They must achieve static equilibrium to prevent soil movement and wall failure. The weight of the retained material exerts a downward force, while the reactive soil pressure on the wall exerts an upward force. By designing the wall and its foundation appropriately, static equilibrium can be maintained, ensuring the stability and integrity of the retaining structure.
4. Dams: Dams are large structures built to hold back water and create reservoirs. Static equilibrium is crucial in their design and construction to withstand the forces exerted by the water pressure. The weight of the dam and the water load must be balanced by the reaction forces from the foundation and the lateral forces from water pressure must be counteracted by appropriate structural design and reinforcement.
In all these examples, achieving static equilibrium is essential to ensure the stability, safety, and functionality of civil engineering structures. By analyzing and balancing the forces and torques acting on the structures, engineers can design and construct them to resist external loads and maintain equilibrium under various conditions.
2.4 Free Body Diagram- Relevant Examples
A free body diagram (FBD) is a visual representation that isolates an object or a system and shows all the external forces acting on it. Here are some relevant examples of free body diagrams:
1. Block on a flat surface: Consider a block resting on a flat surface. The free body diagram of the block would show the following forces:
- The weight of the block acting downward.
- The normal force exerted by the surface, acting upward and perpendicular to the surface.
- If there is friction, the frictional force acting parallel to the surface and opposite to the direction of motion or impending motion.
2. Hanging object: Imagine a mass hanging from a string or a rope. The free body diagram of the hanging object would include:
- The weight of the object acting downward.
- The tension in the string or rope, acting upward and along the direction of the string.
3. Spring-mass system: In a spring-mass system, where a mass is attached to a spring, the free body diagram of the mass would show:
- The weight of the mass acting downward.
- The force exerted by the spring, which is equal and opposite to the displacement of the spring from its equilibrium position.
4. Inclined plane: Consider an object placed on an inclined plane. The free body diagram would show:
- The weight of the object acting vertically downward.
- The normal force exerted by the inclined plane, acting perpendicular to the surface of the plane.
- The component of the weight parallel to the plane, which contributes to the object's motion along the plane.
- If there is friction, the frictional force acting parallel to the plane and opposite to the direction of motion or impending motion.
These examples illustrate the use of free body diagrams to represent the external forces acting on objects or systems. By visualizing and analyzing these forces, engineers and physicists can better understand the forces at play and make accurate calculations and predictions regarding the object's motion and equilibrium.
2.5Equation of Equilibrium in Two/Three Dimensions
The equation of equilibrium in two or three dimensions is derived from Newton's second law of motion, which states that the sum of all forces acting on an object must be zero for it to be in equilibrium. In two dimensions, the equation of equilibrium can be expressed as:
ΣF_x = 0 (sum of all horizontal forces is zero)
ΣF_y = 0 (sum of all vertical forces is zero)
In three dimensions, the equation of equilibrium can be expressed as:
ΣF_x = 0 (sum of all forces along the x-axis is zero)
ΣF_y = 0 (sum of all forces along the y-axis is zero)
ΣF_z = 0 (sum of all forces along the z-axis is zero)
These equations of equilibrium allow engineers and physicists to analyze and solve for the unknown forces acting on an object or system. By setting up and solving these equations, they can determine the conditions necessary for the object or system to be in a state of equilibrium.
2.6 Principle of Transmissibility and Equivalent Forces- Relevant Examples
The principle of transmissibility states that the effects of a force on an object remain unchanged when the force is moved along its line of action. This means that a force can be considered equivalent regardless of its point of application along its line of action. Here are some relevant examples of the principle of transmissibility and equivalent forces:
1. Pushing a car: When pushing a car, the force applied to the car can be considered equivalent regardless of whether it is applied at the front bumper, rear bumper, or any other point along the line of action. As long as the magnitude and direction of the force remain the same, the car will experience the same acceleration and response.
2. Tug of war: In a tug of war game, the force exerted by each team member on the rope is considered equivalent, regardless of their position along the rope. As long as the forces exerted by both teams are equal and opposite, the rope remains in static equilibrium.
3. Lifting an object with a crane: When lifting an object with a crane, the force exerted by the crane's hook on the object is considered equivalent, regardless of the position of the hook along the object. As long as the magnitude and direction of the force remain the same, the object will experience the same upward acceleration and response.
4. Pulling a sled: When pulling a sled with a rope, the force applied to the sled can be considered equivalent, regardless of the specific point along the rope where it is pulled. As long as the magnitude and direction of the force remain the same, the sled will experience the same forward acceleration and response.
In these examples, the principle of transmissibility allows us to simplify the analysis by treating forces as equivalent regardless of their specific point of application along their line of action. This principle is particularly useful in engineering and physics calculations, as it simplifies the analysis of forces and their effects on objects and systems.
2.7Friction Forces: Concept of Static and Dynamic Friction with relevant examples
Friction forces are resistive forces that act between two surfaces in contact. There are two types of friction forces: static friction and dynamic friction.
1. Static friction: Static friction is the frictional force that acts between two surfaces in contact when there is no relative motion between them. It prevents an object from starting to move when a force is applied. The magnitude of static friction can vary depending on the force applied, but it always opposes the impending motion. Examples of static friction include:
- Pushing a heavy box on the floor: When you initially apply a force to push a heavy box, the static friction force between the box and the floor prevents it from sliding. The force you apply must overcome the maximum static friction to set the box in motion.
- Starting a car on a hill: When starting a car on an uphill slope, the static friction between the tires and the road surface prevents the car from rolling backward. The engine must generate enough torque to overcome the static friction and propel the car forward.
2. Dynamic friction: Dynamic friction, also known as kinetic friction, is the frictional force that acts between two surfaces in relative motion. It opposes the motion and acts to slow down or stop the moving object. The magnitude of dynamic friction is typically slightly lower than static friction. Examples of dynamic friction include:
- Sliding a book on a table: When you slide a book on a table, dynamic friction acts between the book and the table surface. It provides the resistive force that opposes the motion and determines the rate at which the book slows down.
- Braking a car: When you apply the brakes in a car, the brake pads exert a force on the rotating wheels, creating dynamic friction. This friction force between the brake pads and the wheels slows down the car's motion by converting its kinetic energy into heat.
- Skidding on an icy road: When a vehicle skids on an icy road, the dynamic friction between the tires and the road surface is significantly reduced. This lack of sufficient friction makes it challenging to control the vehicle's motion and can result in loss of control.
Understanding static and dynamic friction is essential for various applications, such as designing efficient braking systems, predicting the forces required for motion, and ensuring safety in various situations involving contact between surfaces.
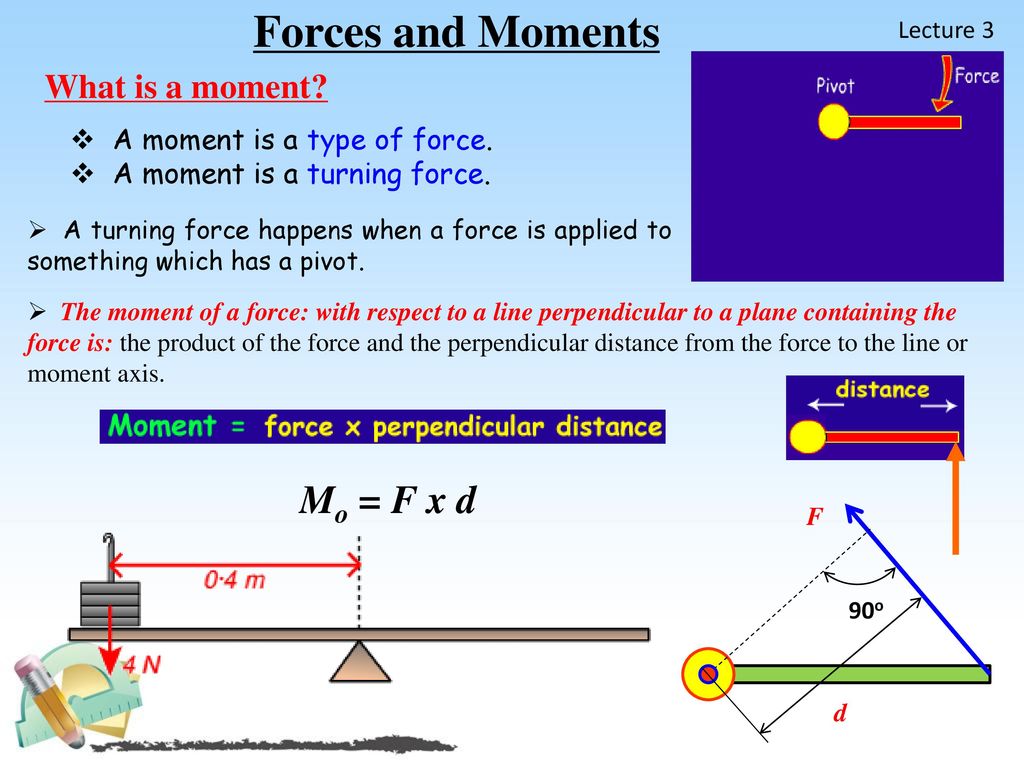
2.8Moments and Couples: Moment of a Force about a point and an axis, theory of couples- Relevant Examples
Moments and couples are concepts related to rotational forces. Here are relevant examples of moments and couples:
1. Moment of a force about a point: The moment of a force about a point is a measure of the tendency of the force to cause rotation around that point. It is calculated by multiplying the magnitude of the force by the perpendicular distance from the point to the line of action of the force. Examples include:
- Opening a door: When you push or pull a door about its hinges, you apply a moment to it. The farther away you push or pull from the hinges, the greater the moment and the easier it is to rotate the door.
- Turning a wrench: When you apply a force to turn a wrench, the moment created is proportional to the force magnitude and the length of the wrench handle. A longer handle provides more leverage and increases the moment for a given force.
2. Moment of a force about an axis: The moment of a force about an axis is similar to the moment about a point, but it considers the perpendicular distance between the axis of rotation and the line of action of the force. Examples include:
- Torque in a rotating shaft: In a machine or engine, a rotating shaft experiences torque, which is the moment of the forces acting on it. Torque determines the rotational motion and power transmission capabilities of the shaft.
- Axle of a car: When a car turns, the forces acting on the tires create moments about the car's axle. The moments help to initiate and control the car's rotational motion during a turn.
3. Theory of couples: A couple is a system of two equal and opposite forces acting on a body but not along the same line of action. Couples produce only rotational effects without any translational motion. Examples include:
- Opening a bottle cap: When you apply a force in opposite directions on a bottle cap, as in a twisting motion, a couple is created. The equal and opposite forces create a rotational effect to loosen or tighten the cap.
- Balancing beams: In a balancing beam or lever system, couples are used to maintain equilibrium. By applying equal and opposite forces at different distances from the fulcrum, the system remains balanced and can be used to lift or move heavy loads.
Understanding moments and couples is crucial in engineering applications such as structural analysis, mechanical systems, and rotational motion. They help in determining stability, calculating torque and rotational forces, and designing mechanisms that rely on rotational effects.
2.9 Resolution of a Force into Forces and a Couple- Relevant Examples
The resolution of a force into forces and a couple involves breaking down a single force into two components: one that creates translational motion (resultant force) and another that creates rotational motion (couple). Here are some relevant examples of resolving a force into forces and a couple:
1. Leaning ladder: Consider a leaning ladder against a wall. The weight of the ladder creates a force that can be resolved into two components:
- Vertical force: The vertical component of the weight supports the ladder's weight and prevents it from falling vertically downward.
- Horizontal force: The horizontal component of the weight creates a moment or couple that tends to rotate the ladder and make it unstable. To prevent the ladder from tipping over, an external force or friction must counteract this rotational effect.
2. Beam supported by a hinge: Imagine a beam supported by a hinge at one end. When a load is applied to the beam, the force from the load can be resolved into two components:
- Vertical force: The vertical component of the load supports the weight of the beam and any additional loads acting vertically downward.
- Horizontal couple: The horizontal component of the load creates a couple or moment that causes the beam to rotate around the hinge. This rotational effect can be countered by applying an equal and opposite couple or by using additional supports.
3. Force applied to a wrench: When a force is applied to a wrench at a distance from the bolt, the force can be resolved into two components:
- Translational force: The component of the force along the wrench's handle creates a translational force that is responsible for turning the bolt.
- Couple: The perpendicular component of the force creates a couple or moment that applies a twisting effect on the bolt. This twisting effect helps to tighten or loosen the bolt.
In these examples, resolving a force into forces and a couple helps in analyzing the different effects of the force on an object. By separating the force into its translational and rotational components, engineers can better understand and address the stability, equilibrium, and motion of the system.
2.10 Resultant of Force and Moment for a System of Force: Examples
The resultant of force and moment for a system of forces refers to the combined effect of all the forces and moments acting on an object or system. Here are some examples of the resultant of force and moment for a system of forces:
1. Structural analysis: In civil engineering, when analyzing the stability and structural integrity of a building or bridge, the resultant of all the forces and moments acting on the structure must be determined. This includes the vertical and horizontal forces from the loads, the reactions from the supports, and any moments caused by imbalances or external factors. By calculating the resultant of these forces and moments, engineers can assess the overall stability and design appropriate structural elements.
2. Aerospace engineering: In the design and analysis of aircraft and spacecraft, the resultant of forces and moments is crucial for flight dynamics. This includes the forces acting on the aircraft such as lift, weight, thrust, and drag, as well as the moments caused by control surfaces, engine thrust, and asymmetrical loading. By considering the resultant of these forces and moments, engineers can evaluate the stability, control, and performance of the aircraft.
3. Mechanical systems: In mechanical engineering, systems such as gears, linkages, and machines often involve multiple forces and moments. By considering the resultant of these forces and moments, engineers can assess the overall behavior and performance of the system. This includes the forces transmitted through gears, the reactions and torques in a linkage system, and the resultant forces and moments on machine components.
4. Automotive engineering: When analyzing the motion and stability of a vehicle, the resultant of forces and moments is essential. This includes the forces from the tires, suspension, and braking systems, as well as the moments caused by weight distribution, aerodynamic forces, and turning forces. By considering the resultant of these forces and moments, engineers can optimize vehicle performance, handling, and safety.
By calculating the resultant of forces and moments in these and other systems, engineers can better understand the overall behavior, stability, and equilibrium of the objects or systems under consideration. This information is crucial for design, analysis, and optimization in various fields of engineering.